This section explains the internal workings of the FrequencyShifter.
It is well known that the maximum bandwidth (Nyquist rate) of a linear sampled system is half the sampling frequency. The nonlinear system used in this project could not be discretized, so numerical methods - central difference and fourth order Runge-Kutta - are employed to solve the differential equation. These approximations inevitably introduce errors. Normalisation (see search normalisation) can be used to improve the responses, but the maximum frequency that can be represented is still significantly lower than the Nyquist frequency of a linear system.
We use frequency shifting to extend the frequency range up to the Nyquist rate. For each combination of numerical method (central difference or Runge-Kutta) and normalisation (search normalised or unnormalised), a maximum frequency is defined. If the user asks for detectors at frequencies higher than this maximum, a version of the input signal which has been modulated down is sent to these detectors and the characteristic frequencies are adjusted suitably.
For each detector, a DetectorBank::detector_components structure is created, which contains the user-specifed input frequency, the characteristic frequency which will actually be used (i.e. the adjusted frequency, or, if no modulation is required, the specified frequency) and the version of the input signal which is to be used by that detector. A vector (DetectorBank::db_components) stores each detector's detector_components struct. This vector is managed by DetectorBank::set_db_components which must be invoked explictly whenever the input buffer is changed (as it is by, for example, DetectorBank::setInputBuffer) so that the frequency-shifted versions of the new input signal can be generated.
Frequency shifting can be achieved by generating a double sideband (DSB) modulated signal, then subtracting a version of the signal with a 90 \(^{\circ}\) phase shift applied. This leaves only the upper sideband (i.e. a single sideband (SSB) signal). The diagram below shows how a signal, \(g(t)\), frequency-shifted by \(\omega_c / 2\pi\) Hz, is generated from the input signal, \(f(t)\), the phase-shifted signal and the sine and cosine of the desired shifting frequency.
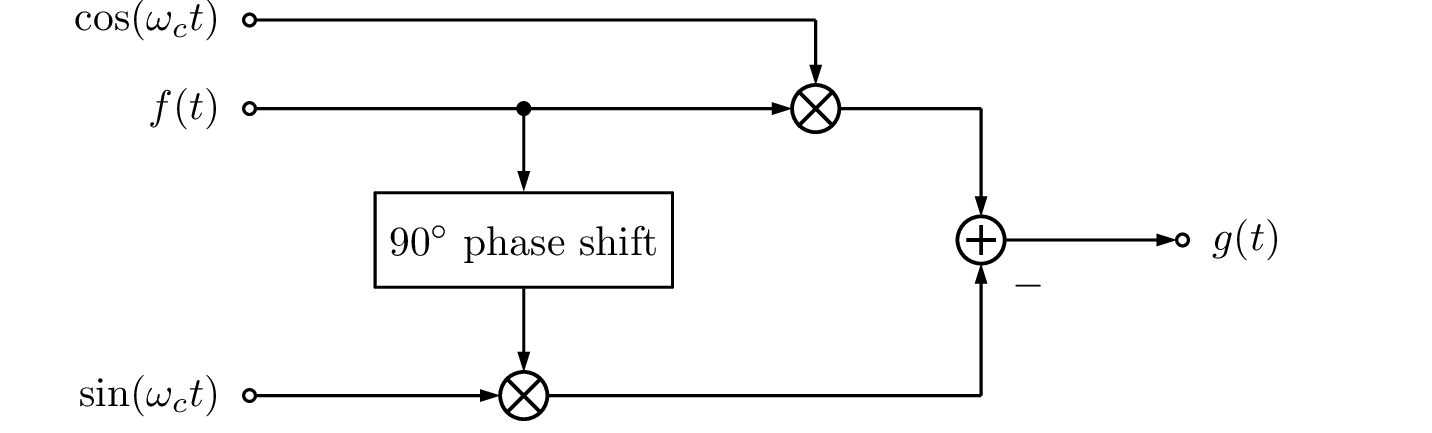
A 90 \(^{\circ}\) phase shift at all frequencies can be implemented with a Hilbert transform. The Hilbert transform of a real signal, \(f(t)\), can be expressed as
\[ f_H(x) = \int_{-\infty}^{\infty} f(t) g(x-t) \; \mathrm{dt} \]
where \(g(x) = - 1/\pi x\), which is simply a convolution and so can be implemented with a Finite Impulse Response (FIR) filter, which is provided by default by the FrequencyShifter.
A method of calculating the Hilbert transform using the Fast Fourier Transform is also supplied. This works by taking the FFT of the signal, setting the negative frequencies to zero then taking the inverse FFT. The result of this is known as the analytic signal: \(m_c = m_r + j m_i\), where \(m_c\) is the (complex) analytic signal, \(m_r\) is the original signal and \(m_i\) is the Hilbert transformed signal. Therefore, performing the above procedure and taking the imaginary part of the result yields the Hilbert transform of the signal.
However, FFTs require the signal to be windowed, so this method does not work for short input buffers, e.g. realtime input. In this situation, FIR method of calculating the Hilbert transform should be used.
- See also
- A word on sample rates
 1.8.13
1.8.13